The TikZ and PGF Packages
Manual for version 3.1.9a

\usegdlibrary{circular} % LaTeX and plain TeX
\usegdlibrary[circular] % ConTeXt

“Circular” graph drawing algorithms arrange the nodes of a graph on one of more circles.

This simple layout arranges the nodes in a circle, which is especially useful for drawing, well, circles of nodes. The name simple necklace layout is reminiscent of the more general “necklace layout”, a term coined by Speckmann and Verbeek in their paper

• Bettina Speckmann and Kevin Verbeek, Necklace Maps, IEEE Transactions on Visualization and Computer Graphics, 16(6):881–889, 2010.

For a simple necklace layout, the centers of the nodes are placed on a counter-clockwise circle, starting with the first node at the grow direction (for grow', the circle is clockwise). The order of the nodes is the order in which they appear in the graph, the edges are not taken into consideration, unless the componentwise option is given.

copy \usetikzlibrary {arrows.meta,graphs,graphdrawing} \usegdlibrary {circular}
\tikz[>={Stealth[round,sep]}]
  \graph [simple necklace layout, grow'=down, node sep=1em,
          nodes={draw,circle}, math nodes]
  {
    x_1 -> x_2 -> x_3 -> x_4 ->
    x_5 -> "\dots"[draw=none] -> "x_{n-1}" -> x_n -> x_1
  };


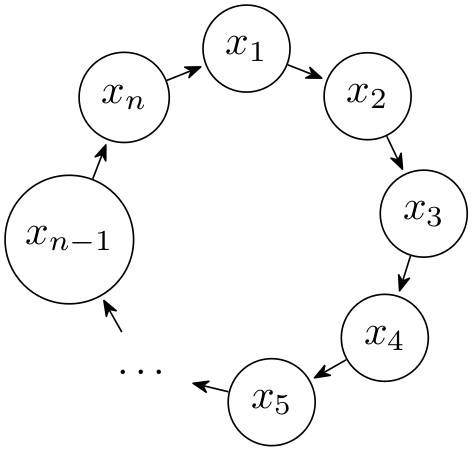
When you give the componentwise option, the graph will be decomposed into connected components, which are then laid out individually and packed using the usual component packing mechanisms:

copy \usetikzlibrary {graphs,graphdrawing} \usegdlibrary {circular}
\tikz \graph [simple necklace layout] {
  a -- b -- c -- d -- a,
  1 -- 2 -- 3 -- 1
};


copy \usetikzlibrary {graphs,graphdrawing} \usegdlibrary {circular}
\tikz \graph [simple necklace layout, componentwise] {
  a -- b -- c -- d -- a,
  1 -- 2 -- 3 -- 1
};


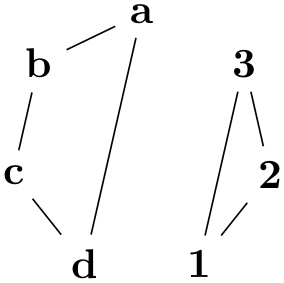
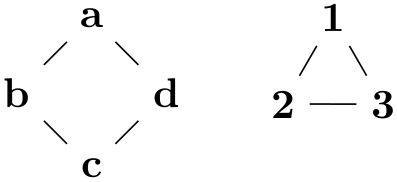
The nodes are placed in such a way that

1. The (angular) distance between the centers of consecutive nodes is at least node distance,

2. the distance between the borders of consecutive nodes is at least node sep, and

3. the radius is at least radius.

The radius of the circle is chosen near-minimal such that the above properties are satisfied. To be more precise, if all nodes are circles, the radius is chosen optimally while for, say, rectangular nodes there may be too much space between the nodes in order to satisfy the second condition.

Examples

copy
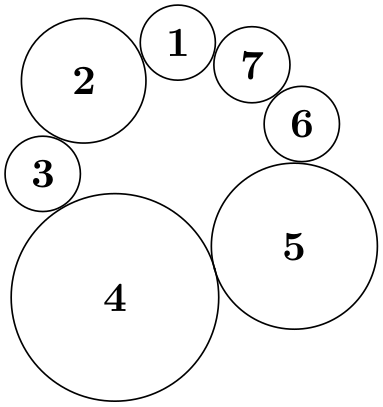
\tikz \graph [simple necklace layout,
              node sep=0pt, node distance=0pt,
              nodes={draw,circle}]
{ 1 -- 2 [minimum size=30pt] -- 3 --
  4 [minimum size=50pt] -- 5 [minimum size=40pt] -- 6 -- 7 };


copy
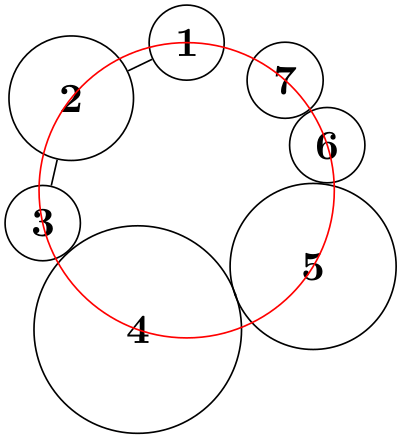
\begin{tikzpicture}[radius=1.25cm]
  \graph [simple necklace layout,
          node sep=0pt, node distance=0pt,
          nodes={draw,circle}]
  { 1 -- 2 [minimum size=30pt] -- 3 --
    4 [minimum size=50pt] -- 5 [minimum size=40pt] -- 6 -- 7 };

  \draw [red] (0,-1.25) circle [];
\end{tikzpicture}


copy
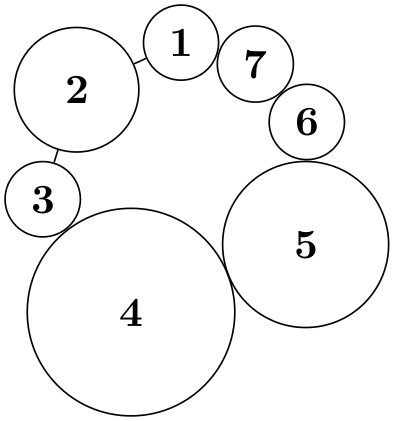
\tikz \graph [simple necklace layout,
              node sep=0pt, node distance=1cm,
              nodes={draw,circle}]
{ 1 -- 2 [minimum size=30pt] -- 3 --
  4 [minimum size=50pt] -- 5 [minimum size=40pt] -- 6 -- 7 };


copy
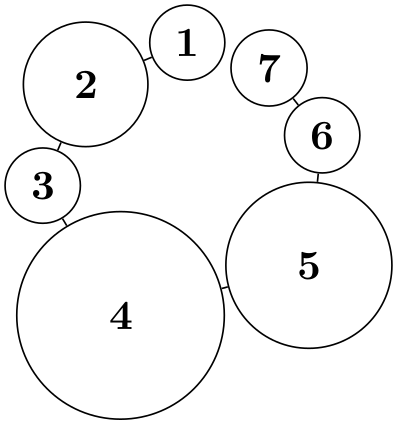
\tikz \graph [simple necklace layout,
              node sep=2pt, node distance=0pt,
              nodes={draw,circle}]
{ 1 -- 2 [minimum size=30pt] -- 3 --
  4 [minimum size=50pt] -- 5 [minimum size=40pt] -- 6 -- 7 };


copy
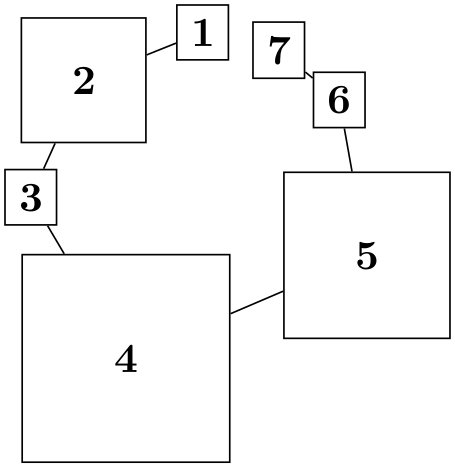
\tikz \graph [simple necklace layout,
              node sep=0pt, node distance=0pt,
              nodes={rectangle,draw}]
{ 1 -- 2 [minimum size=30pt] -- 3 --
  4 [minimum size=50pt] -- 5 [minimum size=40pt] -- 6 -- 7 };